In this post, we shall talk about bias-variance trade-off in machine learning and tips and tricks to avoid overfitting/underfitting. Let’s start with a real-world example.
Fukushima power plant disaster: Failure of predictive modeling
What does a nuclear power plant disaster have to do with machine learning? The safety plan for Fukushima Daiichi nuclear power plant was designed using the historical data for past 400 years. The structural engineers designed the plant to withstand an earthquake of 8.6 intensity on Richter scale and a tsunami as high as 5.7 meters. These threshold numbers were decided using predictive modeling. So, they had the data for earthquakes(intensity and annual frequency) in last 400 years and they were looking for a model that can help predict the earthquakes in future.
The standard method for determining this is Gutenberg-Richter model which fits this on a straight line(linear regression). It shows that an earthquake of intensity 9.0 is likely in 150 years.
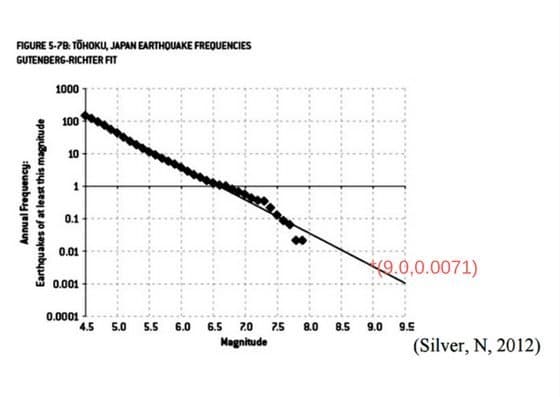
The diamonds represent the actual data while the straight line shows the prediction model as per standard Gutenberg-Richter model
Note that some of the observations(data-points) don’t lie on the prediction graph which is a straight line. However, during the design of Fukushima Daiichi nuclear power plant, the data-scientists used a curve instead of a straight line as the prediction model.
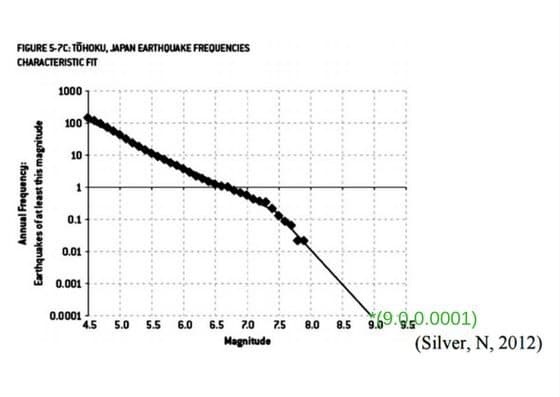
See, how nicely and closely these points fit on the chosen curve. With this prediction model, an earthquake of intensity 9.0 was 70 times less likely. On March 11, 2011, Fukushima plant was hit with an earthquake of intensity 9.1 and tsunami of height > 14 meters which resulted in one of the biggest nuclear disasters of our times. This was caused by a poor understanding of what is known as overfitting or high variance problem in supervised machine learning.
Focus on identifying the pattern, not on fitting all the observations:
In Machine Learning, we are not trying to fit the training data but to identify the unknown underlying pattern. Look at this example:
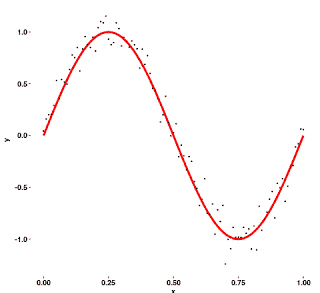
In this example, very few observations lie on our curve but that captures the correct pattern.
In supervised machine learning, there is always a trade-off between approximation and generalization, known as bias-variance trade-off.
What is Bias?:
Whenever we are creating a model using supervised machine learning, we have some training data which contains an underlying pattern which we want to encapsulate in our model and use that to predict for a future(unseen) data-point. Now, if we choose a simple model to predict a complex pattern, our model will have predictions far from actual values, it’s known as underfitting or high bias problem.
A lot of parametric algorithms like linear regression, logistic regression etc suffer from high bias problem. In other words, high bias occurs when our algorithm makes some simplifying assumptions about the underlying unknown pattern.We want our models to have a low bias.
What is Variance?:
Usually, we divide our dataset into three parts:
- Training set: is used for training
- Test Set: for testing
- Validation set: for validation
High variance problem occurs when our model is able to predict well in our training dataset but fails on the test set. In such a case, we say our model is not able to generalize well and has overfitted to the training data. Let’s look at this interesting comic which demonstrates the problem of overfitting by taking an example of American President.

More example of overfitting:
In the example below, our model needs to identify a boundary that can separate blue points from the red ones. In the first(underfitting) example, we have a very loose boundary that wrongly classifies the red points as blue. However, in the third example(overfitting), we are going out of our way to separate each and every observation correctly which results in a boundary which will not work well for a new dataset or observation.
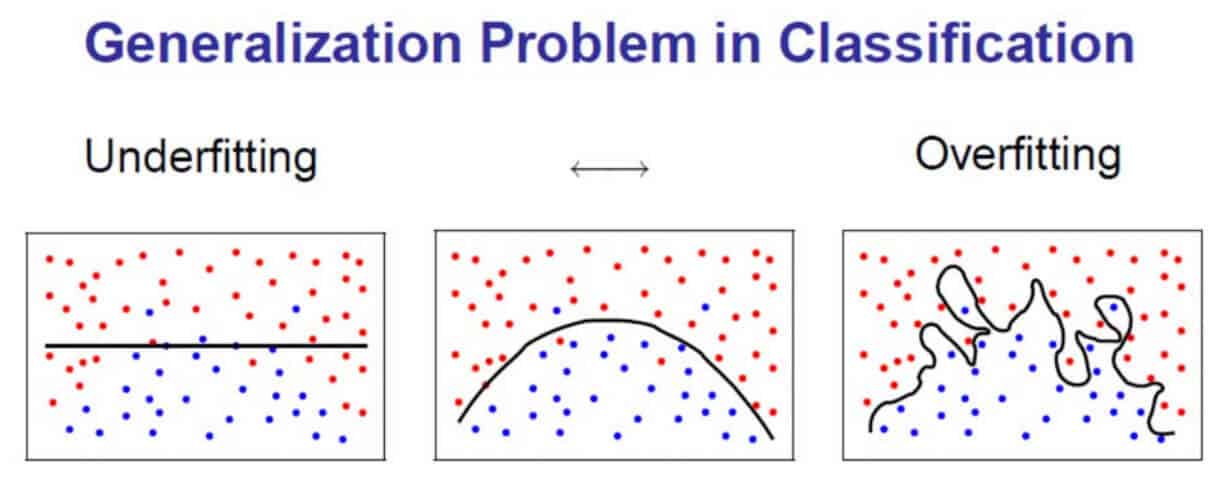
Bias-Variance trade-off:
So, if we choose a more complicated algorithm, we run a risk of high variance problem while if we use a simple one, we will face high bias problem. It’s a double-edged sword. The total error in any supervised machine learning prediction is the sum of the bias term in your model, variance and irreducible error. The irreducible error is also known as Baye’s error or optimum error as it’s mostly noise which can’t be reduced by algorithms but by better data cleaning.
Total error = Bias Term + Variance + Irreducible error
If we plot these values against model complexity, we shall see that at a certain optimum model complexity, we will have the minimum total error.
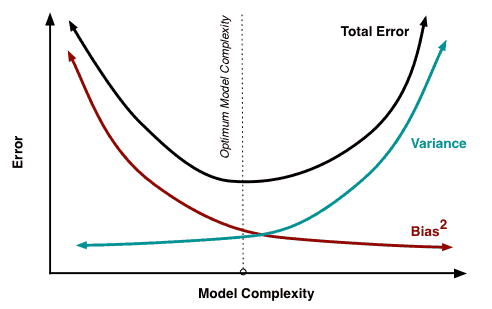
Bias-Variance trade-off while training Neural Networks:
While training neural networks, we encounter underfitting and overfitting very frequently. How do we use the above understanding to improve our training methodology?
During the training of neural networks, here are a few important factors:
- Amount of Training data: If you have very little training data, it’s possible for a network to very easily overfit and learn something else that you want it to. With very little training data, another thing to watch out for is that it must have enough examples so that our model is able to identify the pattern.
- The complexity of Neural network architecture: More complex models, generally have high discriminating ability so, it’s possible to learn more complicated behaviors but they tend to need more training data. For example, it’s possible to model almost any kind of observation using neural networks but if you have little training data, it would result in high bias or underfitting kind of situation.
- Regularization: Regularization techniques such as drop out make it difficult for even a complicated network to overfit.
How to identify and avoid overfitting/underfitting?:
First thing, one should always monitor validation accuracy along with training accuracy. If training accuracy is high(i.e. Training loss is low) but validation accuracy is low(i.e. Validation loss is high), it indicates overfitting. In this case, we should:
- Increase regularization
- Get more training data
If training accuracy itself is low(or training loss is high), then we need to think about:
- Have we done sufficient training?
- Should we train a more powerful network?
- Decrease regularization?
References and image credits:
- https://tomrobertshaw.net/2015/12/introduction-to-machine-learning-with-naive-bayes/
- http://xkcd.com
- http://scott.fortmann-roe.com/docs/BiasVariance.html
- https://mpra.ub.uni-muenchen.de/69383/